How to Read Whitman's Sampler Expiration Date
How To Resample and Interpolate Your Time Series Data With Python
Last Updated on February eleven, 2020
You may have observations at the wrong frequency.
Maybe they are too granular or non granular enough. The Pandas library in Python provides the capability to change the frequency of your time series data.
In this tutorial, y'all will discover how to employ Pandas in Python to both increment and decrease the sampling frequency of fourth dimension series information.
Later completing this tutorial, you will know:
- About time series resampling, the 2 types of resampling, and the 2 chief reasons why you lot need to use them.
- How to use Pandas to upsample fourth dimension series data to a college frequency and interpolate the new observations.
- How to use Pandas to downsample time series data to a lower frequency and summarize the higher frequency observations.
Kick-start your project with my new book Time Serial Forecasting With Python, including step-past-step tutorials and the Python source code files for all examples.
Let's go started.
- Update Dec/2016: Fixed definitions of upsample and downsample.
- Updated Apr/2019: Updated the link to dataset.
How To Resample and Interpolate Your Time Serial Data With Python
Photo past sung ming whang, some rights reserved.
Resampling
Resampling involves irresolute the frequency of your time serial observations.
Two types of resampling are:
- Upsampling: Where you increment the frequency of the samples, such every bit from minutes to seconds.
- Downsampling: Where you lot decrease the frequency of the samples, such equally from days to months.
In both cases, information must be invented.
In the case of upsampling, intendance may be needed in determining how the fine-grained observations are calculated using interpolation. In the case of downsampling, intendance may be needed in selecting the summary statistics used to calculate the new aggregated values.
There are perchance ii chief reasons why you may be interested in resampling your time series data:
- Problem Framing: Resampling may be required if your data is not available at the same frequency that you lot want to make predictions.
- Feature Technology: Resampling can besides be used to provide additional structure or insight into the learning problem for supervised learning models.
There is a lot of overlap betwixt these 2 cases.
For example, you may have daily data and want to predict a monthly problem. You could apply the daily data directly or you could downsample it to monthly information and develop your model.
A feature engineering perspective may use observations and summaries of observations from both time scales and more in developing a model.
Permit'south make resampling more concrete by looking at a real dataset and some examples.
Terminate learning Time Series Forecasting the slow way!
Take my free 7-day email grade and discover how to get started (with sample code).
Click to sign-upwardly and also get a free PDF Ebook version of the course.
Shampoo Sales Dataset
This dataset describes the monthly number of sales of shampoo over a 3 twelvemonth period.
The units are a sales count and there are 36 observations. The original dataset is credited to Makridakis, Wheelwright, and Hyndman (1998).
- Download the dataset.
Below is a sample of the first v rows of data, including the header row.
| "Month","Sales" "i-01",266.0 "1-02",145.nine "1-03",183.one "i-04",119.three "1-05",180.3 |
Beneath is a plot of the unabridged dataset.
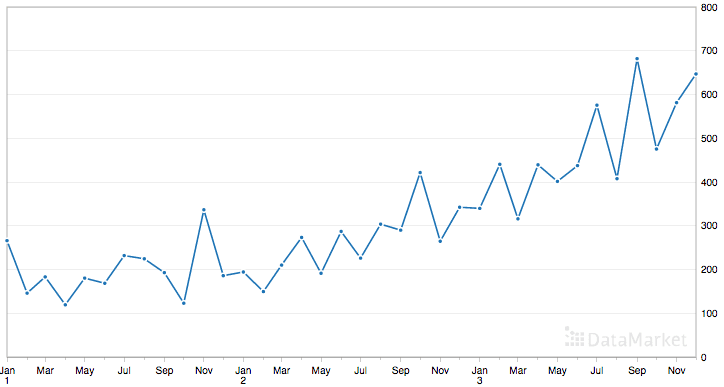
Shampoo Sales Dataset
The dataset shows an increasing tendency and possibly some seasonal components.
Load the Shampoo Sales Dataset
Download the dataset and place information technology in the current working directory with the filename "shampoo-sales.csv".
- Download the dataset.
The timestamps in the dataset do non have an absolute year, simply do accept a month. We tin write a custom date parsing function to load this dataset and pick an capricious year, such as 1900, to baseline the years from.
Below is a snippet of code to load the Shampoo Sales dataset using the custom engagement parsing function from read_csv().
| from pandas import read_csv from pandas import datetime from matplotlib import pyplot def parser ( x ) : render datetime . strptime ( '190' + x , '%Y-%m' ) serial = read_csv ( 'shampoo-sales.csv' , header = 0 , parse_dates = [ 0 ] , index_col = 0 , squeeze = True , date_parser = parser ) print ( series . head ( ) ) series . plot ( ) pyplot . show ( ) |
Running this example loads the dataset and prints the first 5 rows. This shows the correct handling of the dates, baselined from 1900.
| Month 1901-01-01 266.0 1901-02-01 145.ix 1901-03-01 183.ane 1901-04-01 119.iii 1901-05-01 180.3 Name: Sales of shampoo over a three year catamenia, dtype: float64 |
Nosotros also get a plot of the dataset, showing the rising trend in sales from month to month.
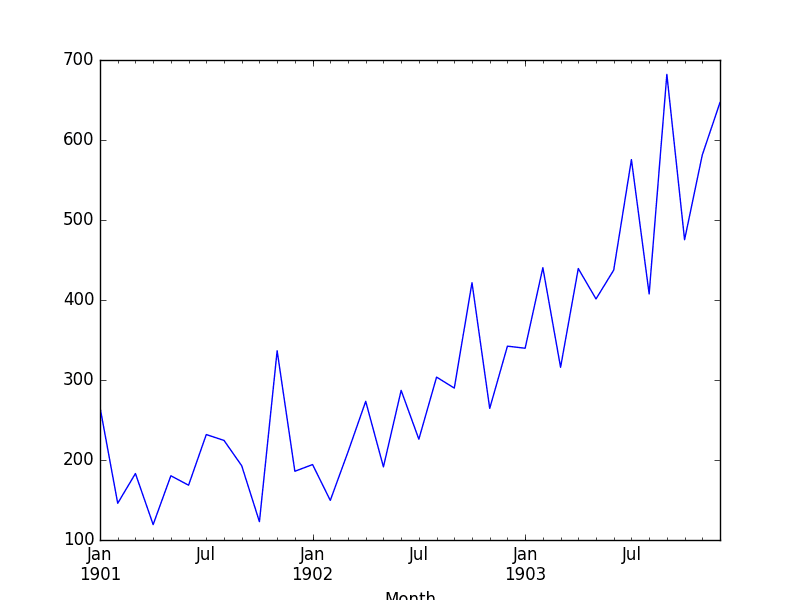
Plot of the Shampoo Sales Dataset
Upsample Shampoo Sales
The observations in the Shampoo Sales are monthly.
Imagine we wanted daily sales information. We would have to upsample the frequency from monthly to daily and apply an interpolation scheme to fill up in the new daily frequency.
The Pandas library provides a part called resample() on the Series and DataFrame objects. This can be used to group records when downsampling and making infinite for new observations when upsampling.
We tin use this function to transform our monthly dataset into a daily dataset by calling resampling and specifying the preferred frequency of calendar twenty-four hour period frequency or "D".
Pandas is clever and you lot could just as easily specify the frequency equally "1D" or fifty-fifty something domain specific, such as "5D." Run into the farther reading section at the end of the tutorial for the list of aliases that you can employ.
| from pandas import read_csv from pandas import datetime def parser ( x ) : render datetime . strptime ( '190' + x , '%Y-%m' ) series = read_csv ( 'shampoo-sales.csv' , header = 0 , parse_dates = [ 0 ] , index_col = 0 , clasp = True , date_parser = parser ) upsampled = series . resample ( 'D' ) print ( upsampled . head ( 32 ) ) |
Running this case prints the commencement 32 rows of the upsampled dataset, showing each day of Jan and the outset day of February.
| one 2 3 4 5 6 seven eight nine x 11 12 13 14 15 16 17 18 nineteen twenty 21 22 23 24 25 26 27 28 29 30 31 32 33 | Month 1901-01-01 266.0 1901-01-02 NaN 1901-01-03 NaN 1901-01-04 NaN 1901-01-05 NaN 1901-01-06 NaN 1901-01-07 NaN 1901-01-08 NaN 1901-01-09 NaN 1901-01-x NaN 1901-01-xi NaN 1901-01-12 NaN 1901-01-13 NaN 1901-01-14 NaN 1901-01-15 NaN 1901-01-sixteen NaN 1901-01-17 NaN 1901-01-eighteen NaN 1901-01-nineteen NaN 1901-01-20 NaN 1901-01-21 NaN 1901-01-22 NaN 1901-01-23 NaN 1901-01-24 NaN 1901-01-25 NaN 1901-01-26 NaN 1901-01-27 NaN 1901-01-28 NaN 1901-01-29 NaN 1901-01-xxx NaN 1901-01-31 NaN 1901-02-01 145.9 |
We can come across that the resample() function has created the rows by putting NaN values in the new values. We tin see we still take the sales volume on the first of January and February from the original information.
Next, nosotros tin interpolate the missing values at this new frequency.
The Series Pandas object provides an interpolate() function to interpolate missing values, and there is a nice selection of simple and more complex interpolation functions. You lot may have domain knowledge to aid cull how values are to be interpolated.
A skillful starting point is to use a linear interpolation. This draws a straight line betwixt bachelor data, in this case on the showtime of the calendar month, and fills in values at the called frequency from this line.
| from pandas import read_csv from pandas import datetime def parser ( x ) : return datetime . strptime ( '190' + 10 , '%Y-%m' ) serial = read_csv ( 'shampoo-sales.csv' , header = 0 , parse_dates = [ 0 ] , index_col = 0 , squeeze = True , date_parser = parser ) upsampled = series . resample ( 'D' ) interpolated = upsampled . interpolate ( method = 'linear' ) print ( interpolated . head ( 32 ) ) |
Running this example, nosotros can see interpolated values.
| 1 ii 3 4 5 6 7 8 nine 10 xi 12 13 14 fifteen 16 17 18 19 twenty 21 22 23 24 25 26 27 28 29 30 31 32 33 | Month 1901-01-01 266.000000 1901-01-02 262.125806 1901-01-03 258.251613 1901-01-04 254.377419 1901-01-05 250.503226 1901-01-06 246.629032 1901-01-07 242.754839 1901-01-08 238.880645 1901-01-09 235.006452 1901-01-10 231.132258 1901-01-eleven 227.258065 1901-01-12 223.383871 1901-01-13 219.509677 1901-01-14 215.635484 1901-01-15 211.761290 1901-01-sixteen 207.887097 1901-01-17 204.012903 1901-01-18 200.138710 1901-01-19 196.264516 1901-01-20 192.390323 1901-01-21 188.516129 1901-01-22 184.641935 1901-01-23 180.767742 1901-01-24 176.893548 1901-01-25 173.019355 1901-01-26 169.145161 1901-01-27 165.270968 1901-01-28 161.396774 1901-01-29 157.522581 1901-01-30 153.648387 1901-01-31 149.774194 1901-02-01 145.900000 |
Looking at a line plot, nosotros see no difference from plotting the original information every bit the plot already interpolated the values betwixt points to draw the line.
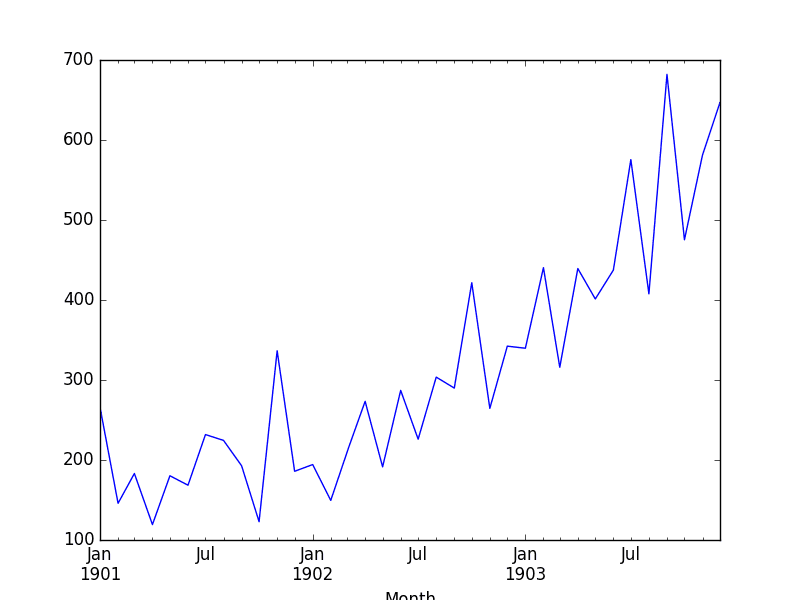
Shampoo Sales Interpolated Linear
Some other mutual interpolation method is to use a polynomial or a spline to connect the values.
This creates more curves and can await more than natural on many datasets. Using a spline interpolation requires you specify the guild (number of terms in the polynomial); in this case, an order of ii is just fine.
| from pandas import read_csv from pandas import datetime from matplotlib import pyplot def parser ( x ) : return datetime . strptime ( '190' + x , '%Y-%m' ) series = read_csv ( 'shampoo-sales.csv' , header = 0 , parse_dates = [ 0 ] , index_col = 0 , squeeze = True , date_parser = parser ) upsampled = serial . resample ( 'D' ) interpolated = upsampled . interpolate ( method = 'spline' , lodge = 2 ) impress ( interpolated . head ( 32 ) ) interpolated . plot ( ) pyplot . show ( ) |
Running the example, we can first review the raw interpolated values.
| ane two iii 4 5 6 vii 8 9 ten eleven 12 13 14 15 16 17 18 nineteen 20 21 22 23 24 25 26 27 28 29 30 31 32 33 | Calendar month 1901-01-01 266.000000 1901-01-02 258.630160 1901-01-03 251.560886 1901-01-04 244.720748 1901-01-05 238.109746 1901-01-06 231.727880 1901-01-07 225.575149 1901-01-08 219.651553 1901-01-09 213.957094 1901-01-10 208.491770 1901-01-11 203.255582 1901-01-12 198.248529 1901-01-xiii 193.470612 1901-01-14 188.921831 1901-01-xv 184.602185 1901-01-16 180.511676 1901-01-17 176.650301 1901-01-18 173.018063 1901-01-nineteen 169.614960 1901-01-20 166.440993 1901-01-21 163.496161 1901-01-22 160.780465 1901-01-23 158.293905 1901-01-24 156.036481 1901-01-25 154.008192 1901-01-26 152.209039 1901-01-27 150.639021 1901-01-28 149.298139 1901-01-29 148.186393 1901-01-30 147.303783 1901-01-31 146.650308 1901-02-01 145.900000 |
Reviewing the line plot, we can see more natural curves on the interpolated values.
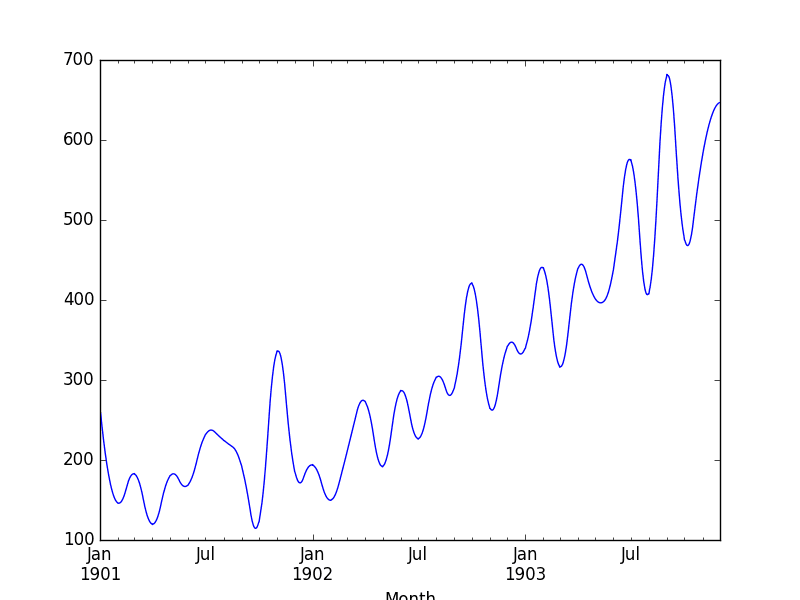
Shampoo Sales Interpolated Spline
Generally, interpolation is a useful tool when y'all have missing observations.
Next, we will consider resampling in the other direction and decreasing the frequency of observations.
Downsample Shampoo Sales
The sales data is monthly, but perhaps we would adopt the information to be quarterly.
The year can exist divided into 4 business organization quarters, iii months a piece.
Instead of creating new rows between existing observations, the resample() function in Pandas will group all observations past the new frequency.
Nosotros could use an alias similar "3M" to create groups of three months, but this might accept trouble if our observations did not start in Jan, Apr, July, or October. Pandas does have a quarter-enlightened allonym of "Q" that we can use for this purpose.
We must at present decide how to create a new quarterly value from each group of iii records. A good starting signal is to calculate the average monthly sales numbers for the quarter. For this, we can apply the hateful() function.
Putting this all together, we go the following code example.
| from pandas import read_csv from pandas import datetime from matplotlib import pyplot def parser ( ten ) : return datetime . strptime ( '190' + ten , '%Y-%thousand' ) series = read_csv ( 'shampoo-sales.csv' , header = 0 , parse_dates = [ 0 ] , index_col = 0 , squeeze = Truthful , date_parser = parser ) resample = series . resample ( 'Q' ) quarterly_mean_sales = resample . mean ( ) impress ( quarterly_mean_sales . head ( ) ) quarterly_mean_sales . plot ( ) pyplot . show ( ) |
Running the case prints the get-go 5 rows of the quarterly information.
| Month 1901-03-31 198.333333 1901-06-30 156.033333 1901-09-xxx 216.366667 1901-12-31 215.100000 1902-03-31 184.633333 Freq: Q-DEC, Proper noun: Sales, dtype: float64 |
We also plot the quarterly information, showing Q1-Q4 beyond the 3 years of original observations.
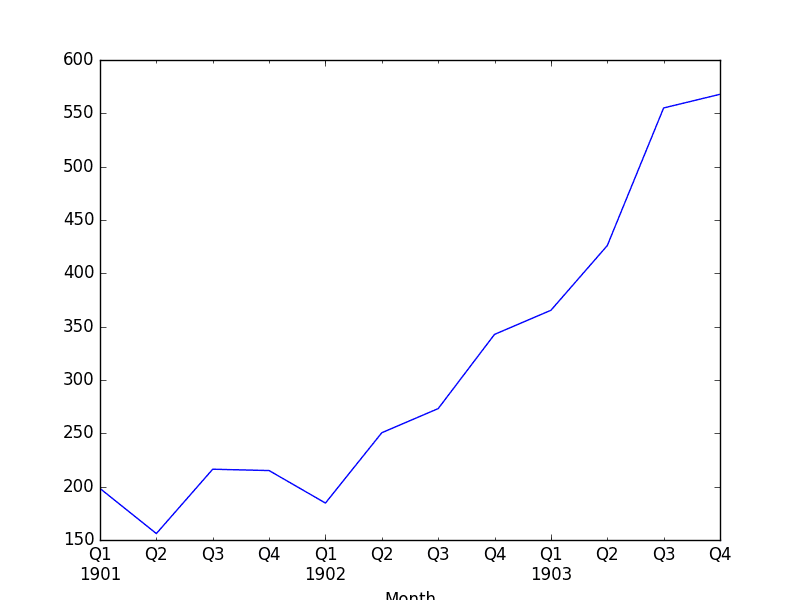
Shampoo Sales Downsampled Quarterly
Perhaps we want to go further and turn the monthly data into yearly data, and perhaps later utilize that to model the following year.
We tin can downsample the data using the alias "A" for twelvemonth-end frequency and this fourth dimension employ sum to summate the total sales each yr.
| from pandas import read_csv from pandas import datetime from matplotlib import pyplot def parser ( x ) : return datetime . strptime ( '190' + 10 , '%Y-%k' ) serial = read_csv ( 'shampoo-sales.csv' , header = 0 , parse_dates = [ 0 ] , index_col = 0 , squeeze = True , date_parser = parser ) resample = series . resample ( 'A' ) quarterly_mean_sales = resample . sum ( ) print ( quarterly_mean_sales . head ( ) ) quarterly_mean_sales . plot ( ) pyplot . testify ( ) |
Running the example shows the 3 records for the 3 years of observations.
We as well get a plot, correctly showing the year along the x-axis and the total number of sales per year along the y-axis.
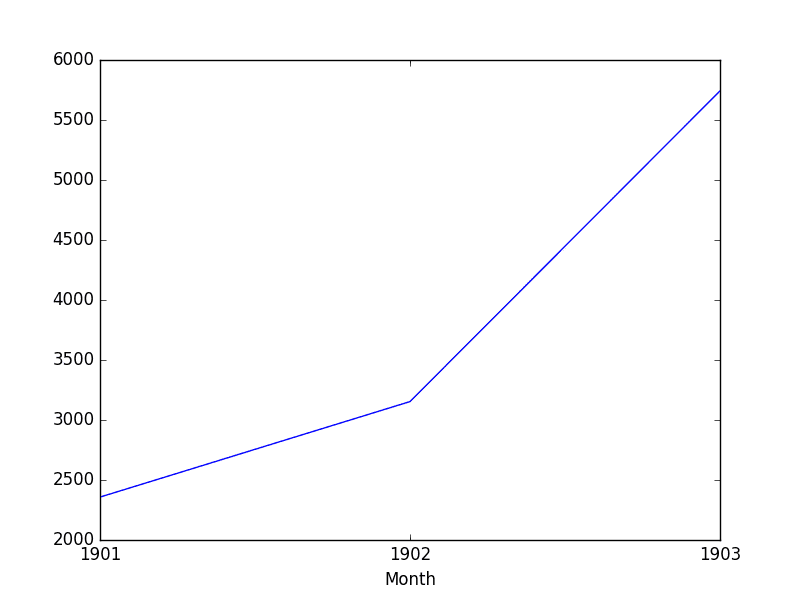
Shampoo Sales Downsampled Yearly Sum
Further Reading
This department provides links and further reading for the Pandas functions used in this tutorial.
- pandas.Series.resample API documentation for more on how to configure the resample() role.
- Pandas Time Series Resampling Examples for more than full general code examples.
- Pandas Offset Aliases used when resampling for all the born methods for changing the granularity of the information.
- pandas.Serial.interpolate API documentation for more than on how to configure the interpolate() function.
Summary
In this tutorial, y'all discovered how to resample your time serial data using Pandas in Python.
Specifically, you learned:
- About fourth dimension serial resampling and the difference and reasons between downsampling and upsampling observation frequencies.
- How to upsample time series information using Pandas and how to use different interpolation schemes.
- How to downsample time serial information using Pandas and how to summarize grouped data.
Practise y'all accept whatever questions about resampling or interpolating time series data or nigh this tutorial?
Ask your questions in the comments and I volition exercise my best to reply them.
Want to Develop Fourth dimension Series Forecasts with Python?
Develop Your Ain Forecasts in Minutes
...with merely a few lines of python code
Observe how in my new Ebook:
Introduction to Time Series Forecasting With Python
Information technology covers self-study tutorials and cease-to-stop projects on topics like: Loading data, visualization, modeling, algorithm tuning, and much more...
Finally Bring Time Series Forecasting to
Your Ain Projects
Skip the Academics. Just Results.
See What'south Inside
Source: https://machinelearningmastery.com/resample-interpolate-time-series-data-python/
0 Response to "How to Read Whitman's Sampler Expiration Date"
Post a Comment